728x90
⬛ 백준 1753번. 최단 경로 - 다익스트라 문풀
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
문제
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
출력
첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.
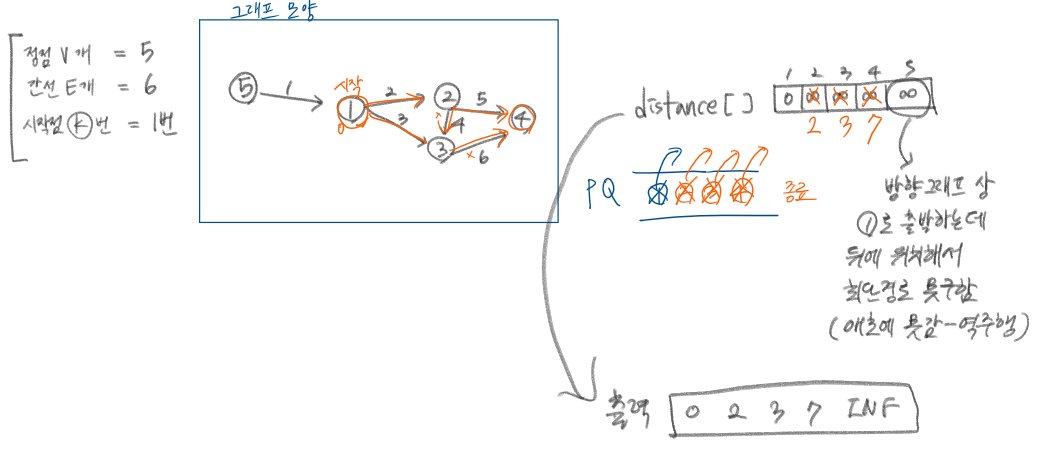
💚 문제 접근 방식
- 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하라고 되어 있다.
- 즉, 한(one) 정점에서 다른 모든(all) 정점으로 갈 최단 경로를 구하라는 전형적인 ‘다익스트라’ 문제이다.
1) 시작 정점 번호는 K로 들어온다.
2) 다익스트라의 핵심은 distance[] 배열과 PriorityQueue 이다.
3) distance[] 정의 : 시작 정점에서부터 다른 모든 all 정점에 대한 최단 경로를 저장할 배열
따라서 태초에는 Integer.MAX_VALUE로 세팅해둔다. (이후 최단 경로 발견할 때마다 갱신할 용도니까 )
4) 시작 정점에 대한 경로는 0으로 세팅해둔다. (왜 ? S→S 자기 자신에 대한 최단 경로는 0)
5) while문으로 PQ가 빌 때까지 순회하면서
현재 cur을 중심으로 방향 그래프 상 cur에 인접한 nx 정점들에 대하여
distance[nx] 기존 거리보다 현재 cur을 경유해서 가는 최단 거리가 더 작을 때 갱신
💚 제출 코드
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Scanner;
/**
* 1753번. 최단 경로 - 다익스트라 문풀
* @author MYLG
*
*/
class Edge implements Comparable<Edge>{
int e, val;
Edge(int e, int val){
this.e = e;
this.val = val;
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return this.val - o.val;//작은 가중치 우선 정렬
}
}
public class Main {
static int V, E, K;
static int[] distance;
static List<ArrayList<Edge>> graph;
//dijkstra
static void dijkstra(int st) { //얘 기준 다른 all 점에 대한 최단 경로
distance = new int[V+1];
Arrays.fill(distance, Integer.MAX_VALUE);
PriorityQueue<Edge> pQ = new PriorityQueue<>();
//시작점 처리
distance[st]= 0;
pQ.offer(new Edge(st, 0));//자기 자신에 대한 거리는 0
while(!pQ.isEmpty()) {
Edge cur = pQ.poll();
for(Edge nx : graph.get(cur.e)) {
if(distance[nx.e] > distance[cur.e] + nx.val) { //다음 정점을 현재 cur 경유해서 세팅하는 게 더 최단 경로라면
//현재 정점 경유해서 더 작은 값 세팅 가능하다면
distance[nx.e] = distance[cur.e] + nx.val;
pQ.offer(new Edge(nx.e, distance[nx.e]));
}
}
}
}
//실행 메인
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner kb= new Scanner(System.in);
V = kb.nextInt();
E = kb.nextInt();
K = kb.nextInt();
graph = new ArrayList<>();
for(int i=0; i<=V; i++) {
graph.add(new ArrayList<>());
}
for(int i=0; i<E; i++) {
int a = kb.nextInt();
int b = kb.nextInt();
//방향 그래프이므로
int val = kb.nextInt();
graph.get(a).add(new Edge(b, val));
}
dijkstra(K);
for(int i=1; i<=V; i++) {
if(distance[i] == Integer.MAX_VALUE) { //닿지 못한 경우
System.out.println("INF");
continue;
}
System.out.println(distance[i]);
}
}
}
728x90
'코딩 테스트 [준비] > [문풀] Baekjoon_백준 문풀_조지기' 카테고리의 다른 글
| 백준 | 11657번. 타임머신 - 최단 경로 (벨만 포드) 문풀 (73) | 2024.01.13 |
|---|---|
| 백준 | 11404번. 플로이드 - 최단경로 (플로이드) 문풀 (72) | 2024.01.13 |
| 백준 | 9251번. 최장 공통 부분 수열(LCS) 찾기 - DP 문풀 (79) | 2024.01.11 |
| 백준 | 1890번. 점프 - DP 문풀 (67) | 2024.01.11 |
| 백준 | 11053번. 가장 긴 증가하는 부분 수열 - DP 문풀 (76) | 2024.01.10 |

