⬛ 백준 2579번. 계단 오르기 - DP 문풀
https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
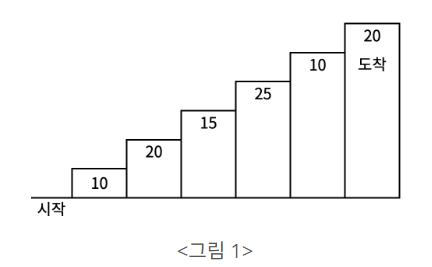
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
💚 문제 접근 방식
- DP 문제는 규칙성을 찾아서 점화식을 구한 뒤, 로직에 구현하는 게 좋다.
- 이 문제의 경우, 1칸 짜리, 2칸 짜리 밟아서 갈 수 있지만, 연속 3칸은 밟으면 안된다고 되어 있다.
- 그럴 땐 3칸 짜리를 어떤 경우의 수로 밟아갈 수 있는지 생각해보고 연속 3칸을 못 밟게 사전 처리를 해두면 된다.
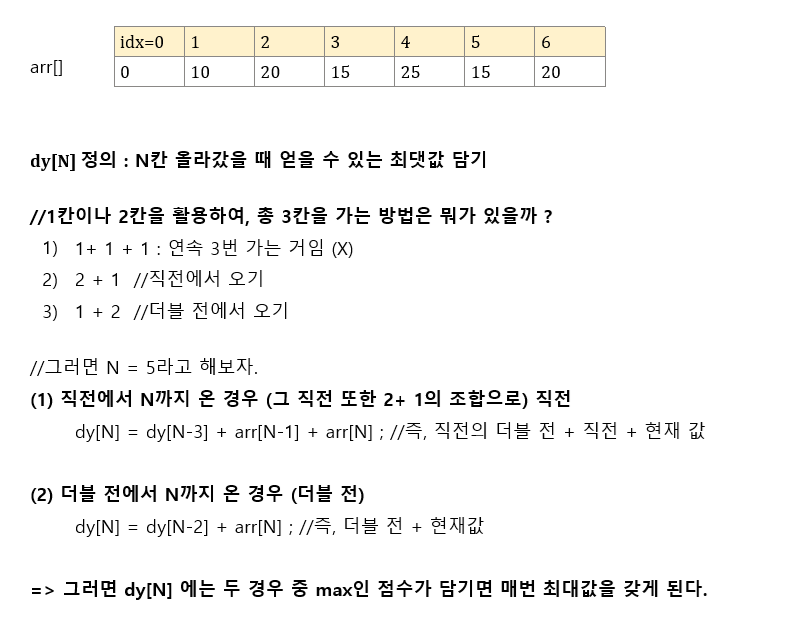
dy[N] 정의 : N칸 올라왔을 때 얻을 수 있는 최대값
dy[N] 점화식 : dy[N] = Math.max( dy[N-2] + arr[N], dy[N-3] + arr[N-1] + arr[N] ) (단, N>=3)
- 최종적으로는 dy[N]을 반환하면 그게 총 N칸 짜리의 계단에서 얻을 수 있는 최대값으로 담겨 문제를 해결할 수 있게 된다.
💚 제출 코드
import java.util.Scanner;
/**
* 백준 2579번. 계단 오르기 - DP 문풀
* @author MYLG
*
*/
public class Main {
//실행 메인
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner kb= new Scanner(System.in);
int N = kb.nextInt();
int[] arr = new int[N+1];
int[] dy = new int[N+1];
for(int i=1; i<=N; i++) {
arr[i]= kb.nextInt();
}
//[주의] : 계단의 개수는 300개 이하 자연수(1~300) 이니까 극단적으로 1이 들어오는 것도 가능함
dy[1] = arr[1];
if(N >= 2) dy[2] = arr[1] + arr[2];
for(int i=3; i<=N; i++) {
//i번째 칸 = 1) 직전 칸(2칸+1칸) + 현재칸 2) 더플 직전칸 (2칸 전) + 현재 칸
dy[i] = Math.max(dy[i-3]+arr[i-1] +arr[i], dy[i-2] + arr[i]);
}
System.out.println(dy[N]);
}
}
'코딩 테스트 [준비] > [문풀] Baekjoon_백준 문풀_조지기' 카테고리의 다른 글
| 백준 | 11053번. 가장 긴 증가하는 부분 수열 - DP 문풀 (76) | 2024.01.10 |
|---|---|
| 백준 | 1912번. 연속합 - DP 문풀 (68) | 2024.01.08 |
| 백준 | 2110번. 공유기 설치 - 이분 탐색 문풀 (62) | 2024.01.06 |
| 백준 | 2805번. 나무 자르기 - 이분 탐색 문풀 (62) | 2024.01.06 |
| 백준 | 2580번. 스도쿠 - 백트래킹(DFS) 문풀 (61) | 2024.01.04 |

