728x90
⬛ 프로그래머스 (카카오 기출) | LV.3 표현 가능한 이진트리 - 분할 정복 & 재귀 문풀
https://school.programmers.co.kr/learn/courses/30/lessons/150367
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr


💚 문제 설명 이해

💚 예제 설명
- 포화 이진 트리를 구성할 수 있는 개수는 다음과 같다.


1) 58 을 표현하기

2) 7 을 표현하기
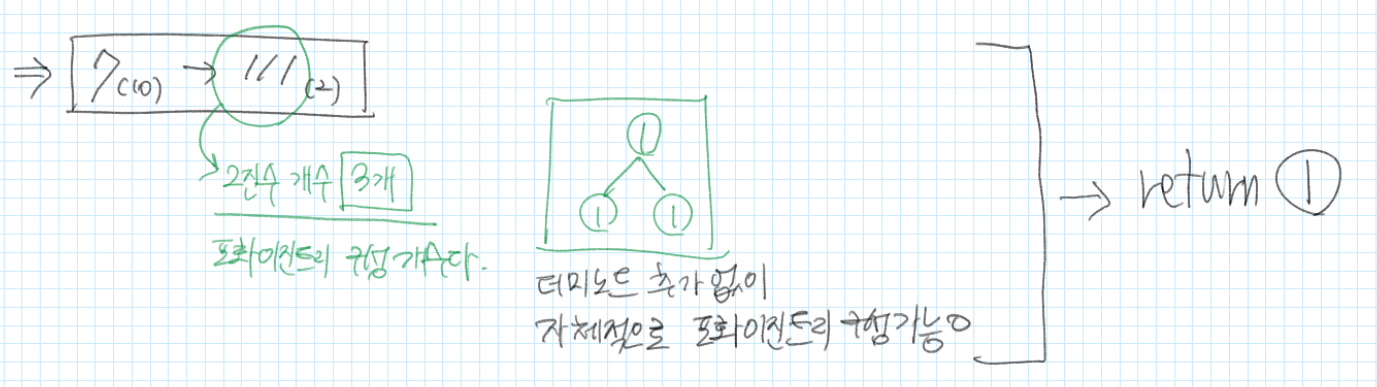
3) 42 를 표현하기

4) 5를 표현하기

5) 95를 표현하기

[풀이 순서]

1) number → 이진수 변환
2) 더미노드를 현재 이진수 str 앞에 (0개~ 현재.lengt()-1 개수만큼)) 하나씩 추가해가면서
2-1) 현재 이진트리의 개수가 포화이진트리 구성 가능한 개수인지 체크
2-2) 만족한다면 실제 포화이진트리 구성이 가능한 구성인지 체크
→ mid중앙값이 1인 경우, 현재 노드의 왼쪽, 오른쪽 자식 부분의 구성도 논리적으로 맞는지재귀적으로 확인
→ mid중앙값이 1이 아닌 경우, 현재 노드의 왼쪽, 오른쪽 자식 부분의 구성에 1 포함 여부 확인
💚 제출 코드
import java.util.*;
class Solution {
//포화 가능한 개수
List<Integer> perfectCountList = Arrays.asList(1, 3, 7, 15, 31, 63);
//솔루션 함수
public List<Integer> solution(long[] numbers) {
List<Integer> answer = new ArrayList<>();
for(long number : numbers){
answer.add(solution(number));
}
return answer;
}
//하나씩 확인
private int solution(long number){
String binaryStr = Long.toBinaryString(number);
int canPlusDummy = binaryStr.length()-1;//루트 제외 개수만큼이 최대 추가 가능한 개수
for(int i=0; i<=canPlusDummy; i++){
String dummyStr = "";
for(int j=0; j<i; j++){
dummyStr += '0';// 그 개수만큼 이어붙임
}
dummyStr += binaryStr;
//이어붙인 상태에서 1) 구성이 (포화이진트리 구성 개수인지) 2) 유효한 구성인지 확인
int dummyLength = dummyStr.length();
if(perfectCountList.contains(dummyLength)){ //가능하다
//유효한 구성인지 확인
if(canPerfectTree(dummyStr)){
return 1;
}
}
}
return 0;
}
//유효한 구성 확인
private boolean canPerfectTree(String dummyStr){
if(dummyStr.length() == 1) return true;
int midIdx = dummyStr.length() /2;
if(dummyStr.charAt(midIdx) == '1'){ //1이면
//그 왼쪽, 오른쪽 서브트리 구성도 유효해야 맞음
String left = dummyStr.substring(0, midIdx);
String right = dummyStr.substring(midIdx+1);
return canPerfectTree(left) && canPerfectTree(right);
}else{ // 0이면
//하위 구성에서 1이 발견되면 안됨 모두 0이어야 함
if(dummyStr.contains("1")) return false;
else return true;
}
}
}
💚 회고
1. 모든 예시가 적용된 과정을 완벽히 이해한 상태여야 엣지 케이스를 모두 고려할 수 있다.
문제가 주는 예시 중 쓸데없는 예시는 없다.
어려운 문제일수록 모든 예시를 직접 손으로 그려보고 그걸 최대한 활용할 수 있어야 한다.
모르겠으면 포기하지말고, 이해해보려는 최소한의 노력이라도 해야 실마리가 나온다. 이 문제의 경우도 그렇다.
2. 처음부터 문제를 읽자마자 '적용할 알고리즘'이 바로 떠오르는 문제는 앞으로도 거의 없을 거다.
특히 어려운 문제일수록 예시와 문제를 이해하는 과정이 필수적이다. 그 흐름을 잘 따라가는 과정에서 특정 알고리즘을 적용할 여지가 보이는 것이다.
ex. 딱 보자마자 BFS다! 딱 보자마자 재귀다 ! 하는 문제들은 그냥 거저 주는 문제라 보통 무조건 맞아야 하는 문제임 만약 변별력 있는 문제를 맞추지 못하는 상태라면 계속 떨어지는 거다.
적용할 알고리즘의 여지가 보일 때마다 더 나은 방식으로 구현할 방법은 없는지 한번 더 고민해봐야 한다.
그 과정이 진화될수록 제출한 코드가 출제자의 목적에 맞게 구현된 코드일 확률이 높다.
3. 엣지 케이스를 놓친 상태로 백날 열심히 구현해봤자 아무 소용 없다.
어렵든 쉽든 그렇다. 예제에서 통과하고 실제 제출 시 통과를 못하면 코드 한줄도 못써낸 사람과 하등 다를 게 없다.
작은 차이같지만 엣지케이스를 놓치는 사람은 계속 떨어지고, 엣지 케이스까지 고려하는 사람은 계속 붙는다.
4. 접근 제한자나 코드 구성에 논리적인 이유가 없으면 안된다.
나중에 면접가서 왜 그렇게 짰는지도 물어볼텐데, 그렇게 물어봤을 때 면접관을 타당한 이유로 설득할 수 없으면 면접까지 겨우가서도 어차피 떨어질거다.
728x90
'코딩 테스트 [준비] > [문풀] 프로그래머스_문풀_조지기' 카테고리의 다른 글
| 프로그래머스 (카카오 기출) | LV.2 문자열 압축 - 문자열 활용 구현 문풀 (Java) (59) | 2024.02.17 |
|---|---|
| 프로그래머스 | LV.1 바탕화면 정리 - 단순 구현 문풀 (Java) (59) | 2024.02.17 |
| 프로그래머스 | LV.2 혼자서 하는 틱택토 - 경우의 수 & 구현 or 완전탐색 문풀 (Java) (76) | 2024.02.08 |
| 프로그래머스 | LV.2 리코쳇 로봇 - BFS 문풀 (Java) (82) | 2024.02.07 |
| 프로그래머스 (카카오 기출) | LV.1 가장 많이 받은 선물 - 단순 구현 문풀 (Java) (83) | 2024.02.07 |

