◼️ 백준 13305번. 주유소
https://www.acmicpc.net/problem/13305
13305번: 주유소
표준 입력으로 다음 정보가 주어진다. 첫 번째 줄에는 도시의 개수를 나타내는 정수 N(2 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 인접한 두 도시를 연결하는 도로의 길이가 제일 왼쪽 도로부터 N-1
www.acmicpc.net
문제
어떤 나라에 N개의 도시가 있다. 이 도시들은 일직선 도로 위에 있다. 편의상 일직선을 수평 방향으로 두자. 제일 왼쪽의 도시에서 제일 오른쪽의 도시로 자동차를 이용하여 이동하려고 한다. 인접한 두 도시 사이의 도로들은 서로 길이가 다를 수 있다. 도로 길이의 단위는 km를 사용한다.
처음 출발할 때 자동차에는 기름이 없어서 주유소에서 기름을 넣고 출발하여야 한다. 기름통의 크기는 무제한이어서 얼마든지 많은 기름을 넣을 수 있다. 도로를 이용하여 이동할 때 1km마다 1리터의 기름을 사용한다. 각 도시에는 단 하나의 주유소가 있으며, 도시 마다 주유소의 리터당 가격은 다를 수 있다. 가격의 단위는 원을 사용한다.
예를 들어, 이 나라에 다음 그림처럼 4개의 도시가 있다고 하자. 원 안에 있는 숫자는 그 도시에 있는 주유소의 리터당 가격이다. 도로 위에 있는 숫자는 도로의 길이를 표시한 것이다.
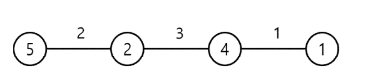
제일 왼쪽 도시에서 6리터의 기름을 넣고, 더 이상의 주유 없이 제일 오른쪽 도시까지 이동하면 총 비용은 30원이다. 만약 제일 왼쪽 도시에서 2리터의 기름을 넣고(2×5 = 10원) 다음 번 도시까지 이동한 후 3리터의 기름을 넣고(3×2 = 6원) 다음 도시에서 1리터의 기름을 넣어(1×4 = 4원) 제일 오른쪽 도시로 이동하면, 총 비용은 20원이다. 또 다른 방법으로 제일 왼쪽 도시에서 2리터의 기름을 넣고(2×5 = 10원) 다음 번 도시까지 이동한 후 4리터의 기름을 넣고(4×2 = 8원) 제일 오른쪽 도시까지 이동하면, 총 비용은 18원이다.
각 도시에 있는 주유소의 기름 가격과, 각 도시를 연결하는 도로의 길이를 입력으로 받아 제일 왼쪽 도시에서 제일 오른쪽 도시로 이동하는 최소의 비용을 계산하는 프로그램을 작성하시오.
입력
표준 입력으로 다음 정보가 주어진다. 첫 번째 줄에는 도시의 개수를 나타내는 정수 N(2 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 인접한 두 도시를 연결하는 도로의 길이가 제일 왼쪽 도로부터 N-1개의 자연수로 주어진다. 다음 줄에는 주유소의 리터당 가격이 제일 왼쪽 도시부터 순서대로 N개의 자연수로 주어진다. 제일 왼쪽 도시부터 제일 오른쪽 도시까지의 거리는 1이상 1,000,000,000 이하의 자연수이다. 리터당 가격은 1 이상 1,000,000,000 이하의 자연수이다.
출력
표준 출력으로 제일 왼쪽 도시에서 제일 오른쪽 도시로 가는 최소 비용을 출력한다.
💚나의 풀이
- 1) 각 주유 가격은 해당 지점을 도착해야 사용 가능하다.
- 2) 첫 번째 주유는 무조건 한다. 마지막 주유 가겨은 사실상 사용 불가하다.
- 3) 왼쪽→오른쪽 최소비용은 매번 가격이 싼 기름으로 갱신시켜서 필요한 거리만큼 충전하면 된다. [그리디]

package to_1026_7;
/*13305번. 다시 풀기 */
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int L[] = new int[N];
int price[] = new int[N];
long min = 1000000000;
long ans = 0;
for (int i = 0; i < N - 1; i++) {
L[i] = sc.nextInt();
}
for (int i = 0; i < N; i++) {
price[i] = sc.nextInt();
}
//min값을 매번 더 작은 값 발견할 때까지 유지하다가 발견하면 갱신하는 형태로
for (int i = 0; i < N-1; i++) {
min = Math.min(min, price[i]);
ans += min*L[i];
}
System.out.println(ans);
}
}
'코딩 테스트 [준비] > [문풀] Baekjoon_백준 문풀_조지기' 카테고리의 다른 글
| 백준 | 14267번. 회사 문화 1 - DFS & DP 문풀 (1) | 2023.11.09 |
|---|---|
| 백준 | 3803번. Networking - 최소 스패닝 트리 문풀 (0) | 2023.11.01 |
| 백준 | 22352번. 항체 인식 - BFS 풀이 (0) | 2023.10.25 |
| 백준 | 4195번. 친구 네트워크 - 유니온 & 파인드, HashMap (0) | 2023.10.11 |
| 백준 | 14502번. 연구소 - DFS & BFS (0) | 2023.10.06 |

