⬛ 백준 13418번. 학교 탐방하기- 최소 스패닝 트리 문풀
https://www.acmicpc.net/problem/13418
13418번: 학교 탐방하기
입력 데이터는 표준 입력을 사용한다. 입력은 1개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에는 건물의 개수 N(1 ≤ N ≤ 1,000)과 도로의 개수 M(1 ≤ M ≤ N(N-1)/2) 이 주어진다. 입력의 두 번
www.acmicpc.net
문제
국민대학교 홍보대사 국희는 여름방학을 맞아 고등학생들을 대상으로 학교 내부에 있는 건물을 소개해주는 일을 하게 되어 학교 건물을 차례로 소개할 수 있는 이동 경로를 짜보기로 하였다. 국민대학교는 북한산의 정기를 받는 위치에 있어 건물 간 연결된 길이 험난한 오르막길일 수도 있고, 내리막길일 수도 있다. 국희는 먼저 입구를 기준으로 건물 간 연결된 도로가 오르막길인지, 내리막길인지를 파악하여 오르막길인 경우 점선, 내리막길인 경우 실선으로 표시하였다.
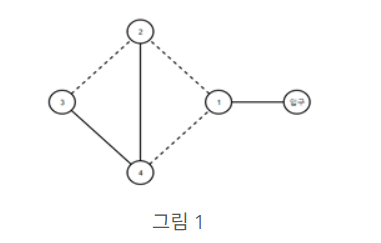
건물을 구분하기 쉽도록 번호를 붙였고, 입구에는 숫자 0을 붙이기로 하였다. 그 다음 모든 건물을 방문하는 데 필요한 최소한의 길을 선택하여, 해당 길을 통해서만 건물들을 소개하기로 하였다. 이 과정은 굉장히 신중해야 하는데, 오르막길이 많이 포함되게 되면 굉장히 피곤해지기 때문이다.
얼마나 피곤해지는지 알아보기 위해 피로도를 계산하기로 하였다. 오르막길을 k번 오를 때, 피로도는 k2이 된다. 피로도의 계산은 최초 조사된 길을 기준으로만 한다. 즉, 내리막길로 내려갔다 다시 올라올 때 오르막길이 되는 경우는 고려하지 않는다. 입구는 항상 1번 건물과 연결된 도로를 가지며, 출발은 항상 입구에서 한다.
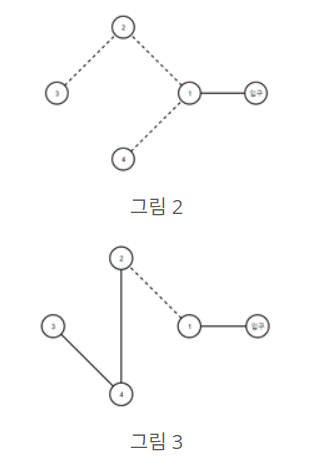
그림 1에서 모든 건물을 소개하기 위해 거쳐야 할 최소한의 도로는 4개임을 알 수 있다. 다음 2개의 그림은 그 4개의 도로를 뽑은 각각의 경우이다. 그림 2는 학교를 소개하는 데 총 3개의 오르막길을 오르게 되며 피로도가 9가 되는 최악의 코스가 된다. 그림 3은 오르막길을 1번만 오르게 되므로 학생들의 피로도는 1이 되는 최적의 코스가 된다. 이 경우 최악의 코스와 최적의 코스간 최종 피로도의 차이는 8이 된다. 국희는 최고의 프로그래머인 당신에게 위와 같은 방식으로 최악, 최선의 경로 간 피로도의 차이를 계산하는 프로그램의 제작을 부탁하였다. 프로그램을 작성하여 국희를 도와주자.
입력
입력 데이터는 표준 입력을 사용한다. 입력은 1개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에는 건물의 개수 N(1 ≤ N ≤ 1,000)과 도로의 개수 M(1 ≤ M ≤ N(N-1)/2) 이 주어진다. 입력의 두 번째 줄부터 M+1개의 줄에는 A, B(1 ≤ A, B ≤ N), C 가 주어진다. 이는 A와 B 건물에 연결된 도로가 있다는 뜻이며, C는 0(오르막길) 또는 1(내리막길)의 값을 가진다. 같은 경로 상에 2개 이상의 도로가 주어지는 경우는 없으며, 입구는 항상 1번 건물과 연결되어 있다. 입구와 1번 도로 간의 연결 관계는 항상 2번째 줄에 주어진다. 입구에서 모든 건물로 갈 수 있음이 보장된다.
출력
출력은 표준 출력을 사용한다. 입력받은 데이터에 대해, 주어진 조건을 만족하는 최악의 경로에서의 피로도와 최적의 경로 간 피로도의 차이를 출력한다.
💚나의 풀이
- pQ를 2개의 버전으로 나누어서 선언했다.
- pQ1 의 경우, 0의 값을 갖는 오르막길을 우선하여 연결하도록 최소비용 (오름차순) 으로 선언했고,
- pQ2 의 경우, 1의 값을 갖는 내리막길을 우선하여 연결하도록 최대비용(내리마순) 으로 선언했다.
- MST() 함수에 각각 사용할 pQ를 인수로 보내고, 똑같이 while문을 걸어서 간선을 연결하면 된다.
- 이때, 시작 정점을 0으로 시작하도록 하려고 했는데, 문제의 조건에서 0과 연결된 것은 1만 있다고 되어 있었으므로, 무조건 모든 정점을 연결하려면 반드시 연결될 것이므로 pQ의 우선 순위 조건에 따라 N-1개의 간선만 연결해두면 된다.
package to_0927_1;
import java.util.PriorityQueue;
import java.util.Scanner;
/*백준 13418번. 학교 탐방하기 - 최소스패닝트리 */
class Edge{
int s, e, val;
Edge(int s, int e, int val){
this.s = s;
this.e = e;
this.val = val;
}
}
public class Main {
static int N, M;//입력 +1처리 해줘야 함
static int[] parent;//부모노드 저장용
//find
static int find(int a) {
if(a == parent[a]) return a;
return parent[a] = find(parent[a]);
}
//union
static void union(int a, int b) {
a = find(a);
b = find(b);
if(a != b) {
parent[b] = a;
}
}
//mst 알고리즘 - 오르막길 0 이 나오는 횟수 카운팅하여 리턴
static int MST(PriorityQueue<Edge> pQ) {
//st에 대한 처리
int useEdge = 0;
int useCost = 0;
while(useEdge < N-1) {
Edge cur = pQ.poll();//하나 뽑아서
if(find(cur.s) != find(cur.e)) {
union(cur.s, cur.e);
useEdge++;
if(cur.val == 0) {
useCost++;//오르막길 개수 ++처리
}
}
}
return useCost;
}
//실행 메인
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner kb= new Scanner(System.in);
//입력값을 보면 0번부터 N번의 N+1개 정점이 들어온다.
//도로는 총 M+1개 들어온다. 이 점을 유의해서 입력값보다 +1 처리 할 것
N = kb.nextInt() + 1;
M = kb.nextInt() + 1;
parent = new int[N];
for(int i=0; i<N; i++) parent[i]= i;
//1) 최악 = 0 (오름차순) 여러 개 나와야 함 - 즉, 최소비용이므로 오름차순 우선 -> a의 가중치 적은 거 우선
PriorityQueue<Edge> pQ1 = new PriorityQueue<>((a, b) -> a.val - b.val);
//2) 최적 = 0 이 최대한 적고 1이 많이 나와야 함 즉. 최대비용이므로 내림차순 운선
PriorityQueue<Edge> pQ2 = new PriorityQueue<>((a, b)-> b.val - a.val);
//데이터 pQ에 입력받기
for(int i=0; i<M; i++) {
int a = kb.nextInt();
int b = kb.nextInt();
int val = kb.nextInt();
//두 개의 큐에 다 담기
pQ1.add(new Edge(a, b, val));
pQ2.add(new Edge(a, b, val));
}
//1) 최악 경로 : 최소비용
int ans1 = MST(pQ1);//0번으로 출발해야 하므로
//Re 초기화
parent = new int[N];
for(int i=0; i<N; i++) parent[i]= i;
//2) 최적 경로 : 최대 비용
int ans2 = MST(pQ2);
int answer = (int) (Math.pow(ans1, 2) - Math.pow(ans2, 2));
System.out.println(answer);
}
}
data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACH5BAEAAAAALAAAAAABAAEAAAICRAEAOw==
'코딩 테스트 [준비] > [문풀] Baekjoon_백준 문풀_조지기' 카테고리의 다른 글
| 백준 | 9370번. 미확인 도착지 - 다익스트라 (0) | 2023.09.27 |
|---|---|
| 백준 | 1414번. 불우이웃돕기 - 최소 스패닝 트리 (0) | 2023.09.27 |
| 백준 | 13905번. 세부 - 최소 스패닝 트리 문풀 (0) | 2023.09.25 |
| 백준 | 4386번. 별자리 만들기 - 최소비용 신장 트리 (0) | 2023.09.11 |
| 백준 | 14621번. 나만 안되는 연애 -최소비용 신장 트리 (1) | 2023.09.11 |

