1절. 확률
[확률]
: 사건이 일어날 수 있는 측정 수치
- 각 사건은 0~1 사이 값 가짐
- 모든 사건 확률의 총합 = 1
[표본공간] : S
- 일어날 수 있는 모든 결과의 집합
[표본점]
- 표본 공간의 원소
[확률 부여 기본조건]
1) 각 확률은 0 – 1 사이 값
2) 모든 확률의 합 = 1
[확률 부여 방법] *시험**
1) 고전적 방법
: 각 확률이 1/n 로 동일한 경우 적합
2) 상대도수적 방법
: 반복 사건일 때 적합
: 반복횟수 올라갈수록 정확도 높아짐
3) 주관적 방법
: 각 확률 1/n (X), 반복 사건 (X) 일 때 적합
: 개인의 경험, 직관력 바탕으로 이용 가능한 모든 정보 고려
: 어떤 사건이 일어날 모든 경우의 수를 고려하고, 특정 결과 나타날 확률을 추정
: 각자가 추정하는 확률이 다르다. (개인적 주관,특성 반영됨)
: 특별한 검토 필요한 방법
2절. 확률 계산 법칙
- [기본]
1) 각 사건 당 경우의 수가 동일 + n회 반복 실험인 경우
- [사건] 동전 던진다 = 앞면 or 뒷면 : ; 각 사건당 2가지 경우의 수 존재
- 이 사건을 3회 반복
즉, 표본공간의 원소의 수 = 2^3
2) 순열: 서로 다른 n개 중, 서로 다른 r개 뽑고, 일렬로 나열
3) 조합: 서로 다른 n개 중, 서로 다른 r개 뽑음
- [사건과 확률]
- 사건 : 표본점들의 집합
- 사건의 확률 : 사건에 부여된 확률들의 합
- [확률 성질]
- [확률 덧셈법칙]
- 합사건
- 곱사건
- [상호배반 사건]
: 두 사건 교집합 X
3절. 조건부확률
[조건부확률]
- 사건 B가 일어났을 때의 사건 A 일어날 확률
[독립사건]
- 사건 A가 사건 B 확률에 전혀 영향 X
- 두 사건의 확률 측정에 서로 사건이 영향 안미치는 거
- 잇달아 나타나는 사건은 서로 영향을 미치는 거.
[확률 곱셈법칙]
4절. 베이즈 정리 (*시험)**
- 사전 확률에 추가 정보 들어온 경우, 이를 베이즈 정리 적용하여 계산한 뒤 ‘사후확률’ 냄
[베이즈 정리 순서]
- 사건의 표본공간 분리 나열
- 사전확률 p(A)
- 조건부확률 p(B|A)
- 결합 확률
- 사후 확률
5절. 이산 확률 분포
- 확률변수 ; 실험결과를 숫자로 표현하는 방식. 숫자에 따라 확률 부여
- [이산확률변수] : 결과가 셀 수 있는 숫자로 표현. 구간X 표현 가능한 확률변수
- cf. [연속확률변수] : 결과가 일정 구간에 연속적인 값을 갖는 확률변수
- [이산확률분포] : 이산 확률변수의 값 따르는 확률들의 나열
- [이산확률변수의 평균과 분산]
- [이항 확률분포] : binom
- dbinom(x , size, p) : 확률값 구하는 함수
- pbinom(x, size, p, lower.tail =T/F) : 누적 확률값 구하는 함수
- qbinom(p, size, p, lower.tail = T/F) : 누적 확률이 p가 되는 x값 구하는 함수
- [포아송 확률분포] : pois
- dpois(x, 평균) : 확률값 구하는 함수
- ppois(x, 평균, lower.tail=T/F) : 누적 확률값 구하는 함수
- qpois(p, 평균, lower.tail=T/F) : 누적 확률이 p가 되는 x값 구하는 함수
- [초기하 확률분포] : hyper
- dhyper(x, m, n, k) : 확률값 구하는 함수
- phyper(x, m, n, k, lower.tail=T/F) : 누적확률값 구하는 함수
- qhyper(p, m, n, k, lower.tail=T/F) : 누적 확률이 p가 되는 x값 구하는 함수
6절. 연속 확률분포
- [균일 분포] : unif
- dunif(x, min, max) : 확률밀도함수 구하는 함수
- punif(q, min, max, lower.tail =T/F) : 누적 확률값 구하는 함수
- qunif(p, min, max, lower.tail =T/F) : 누적 확률이 p가 되는 x값 구하는 함수
- [정규 분포] : norm
- dnorm(x, m, sd) : 확률 밀도 함수 구하기
- pnorm(q, m, sd, lower.tail = T/F) : 누적확률값 구하는 함수
- qnorm(p, m, sd, lower.tail = T/F) : 누적 확률이 p가 되는 x값 구하기
- rnorm(n, m, sd) : 정규 분포를 따르는 난수 생성하기
- [표준 정규 분포] : norm
- dnorm(x, 0, 1) : 확률 밀도 함수 구하기
- pnorm(q, 0, 1, lower.tail = T/F) : 누적확률값 구하는 함수
- qnorm(p, 0, 1, lower.tail = T/F) : 누적 확률이 p가 되는 x값 구하기
- rnorm(n, 0, 1) : 정규 분포를 따르는 난수 생성하기
- [지수 확률분포] : exp
- dexp(x, rate) : 확률 밀도 함수 구하기
- pexp(q, rate, lower.tail = T/F): 누적확률값 구하는 함수
- qexp(p, rate, lower.tail = T/F): 누적 확률이 p가 되는 x값 구하기
- rexp(n, rate) : 지수 분포를 따르는 난수 생성하기
4장 연습문제
15번. 우리 회사의 프린트는 A, B 2대가 있다. 서버 A에는 20명이 연결되어 있고, 서버 B에는 10명이 연결되어 있다. 연결된 직원 5명을 추출하였을 때 아래 질문들을 R로 구현하여라.
(1) 서버 A에 연결된 직원이 한명도 뽑히지 않을 확률은?
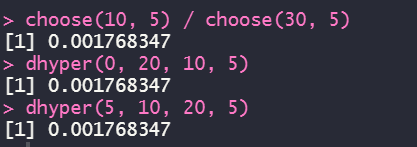
(2) 서버 A에 연결된 직원이 3명 뽑힐 확률은?
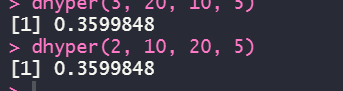
(3) 서버 A에 연결된 직원이 3명 이상 뽑힐 확률은?

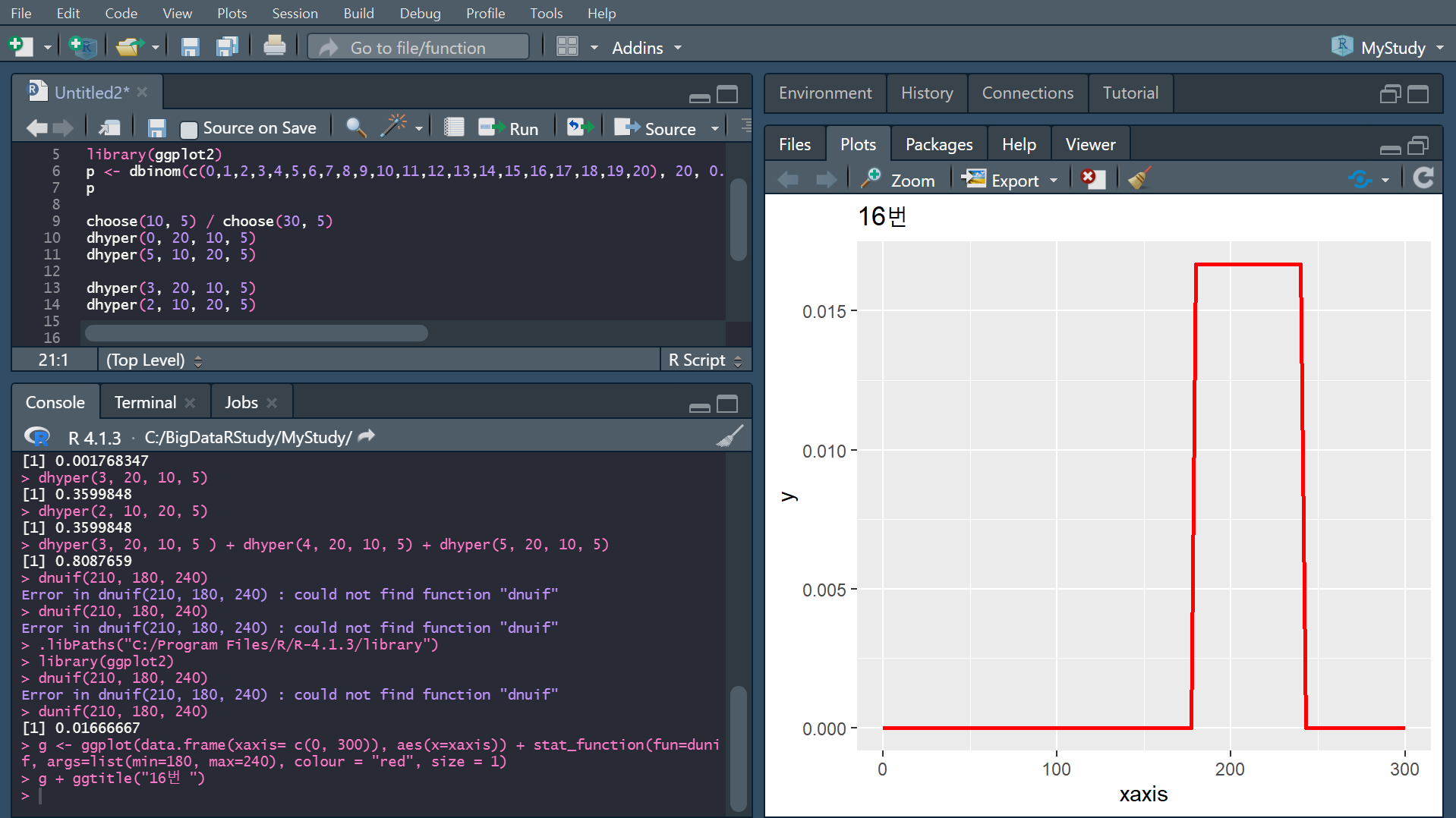
16번. 우리 회사의 인터넷 이용자들의 이용시간은 3분~4분 사이에 랜덤하게 이용한다. 아래 물음들을 R로 구현하여라.
(1) 확률밀도함수는?

(2) 확률밀도 함수 그래프를 그려라

'[전공] 학교 전공 공부 > [학교]_빅데이터 소프트웨어' 카테고리의 다른 글
| ahricolase , car , leaps, forecast 패키지 다운로드 (0) | 2022.06.16 |
|---|---|
| 추정 및 검정 (0) | 2022.04.24 |
| 데이터 시각화 (0) | 2022.04.16 |
| ggplot 패키지 그래프 그리기 (0) | 2022.04.16 |
| ggplot2 패키지 설치 (0) | 2022.04.15 |

